Сопряженная матрица

Пусть  (i=1,2,...,m; j=1,2...,n) и пусть элементы матрицы A комплексные числа. Сопряженной по отношению к A называется матрица 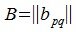 (p=1,2,...,n; q=1,2...,m), где b_pq=a_qp ( a_qp сопряженное значение числа a_qp).

Для обозначения сопряженного к A матрицу используют запись A^*.

Для построения сопряженной матрицы достаточно взять в качестве столбцов − соответствующие строки исходной матрицы (т.е. транспонирование исходной матрицы), с последующей заменой каждого элемента полученной матрицы на соответствующий комплексно-сопряженный элемент. Например:

Свойства сопряженных матриц

1. (A^*)^*=A.
2. Если матрицы A и B одинакового размера, то (A+B)^*=A^*+B^*.
3. Если определено произведение AB (т.е. количество строк A равен количеству столбцов B ), то (AB)^*=B^*A^*.
4. (βA)^*=βA*, где β - произвольное комплексное число, а β число, комплексно сопряженное к β.
5. Если A квадратная матрица, то (A^-1)^*=(A^*)^-1, где A^-1 обратная к A матрица .

Если A− вещественная матрица, т.е. все элементы матрицы A вещественны, то A^*=A^T.

Для операций с матрицами пользуйтесь матричным онлайн калькулятором.