Сложение векторов

Суммой x+y векторов x и y называется вектор, проведенный из начала x к концу у, если вектор у параллельно перемещен так, что конец x и начало y совмещены.

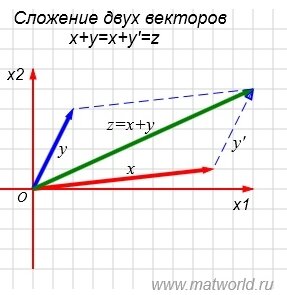
Рис. 1

Вариант 1. Начальные точки всех векторов совпадают с началом координат.

Построим сумму z=x+y векторов и .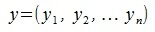

Для построения суммы векторов z=x+y, нужно переместить параллельно вектор y так, чтобы начало вектора y совпало с концом вектора x. Тогда конец полученного вектора y' будет конечной точкой суммы векторов z=x+y.

Таким образом, для получения суммы векторов x и y достаточно сложить соответствующие координаты векторов x и y:

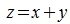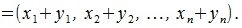На рисунке Рис. 1 в двухмерном пространстве представлен процесс сложения векторов x=(9,1) и y=(2,4).

Вычислим z=x+y=(9+2, 1+4)=(11,5). Сравним полученный результат с геометрической интерпретацией. Действительно, после параллельного перемещения вектора y на позицию y' и сложения x и y', получим вектор z=(11,5).

Вариант 2. Начальные точки векторов произвольные.

Рассмотрим процесс сложения двух векторов x и y. Пусть вектор x имеет начальную точку 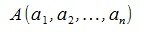и конечную точку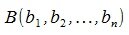, а вектор y - начальную точку 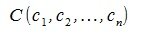и конечную точку 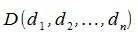. Для того, чтобы параллельно переместить вектор y, нужно каждый элемент i точек C и D увеличить на соответствущую величину γ_i:

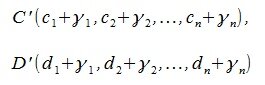(1)

а для того, чтобы точка C переместилась в точку B, должны выполняться условия

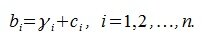(2)

Следовательно

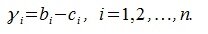(3)

Подставляя (3) в (1), получим:

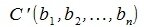	(4)

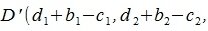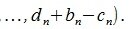Из выражений (4) видно, что точка C' совпала с точкой B, и, следовательно, вектор 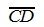переместился в нужную позицию BD'. Таким образом, начальная точка вектора x+y будет точка A, а конечная точка - будет точка D', которая вычисляется из выражения в (4).

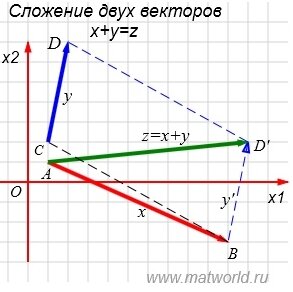
Рис. 2

На рисунке Рис.2, для получения суммы векторов x и y, вектор y перемещается параллельно так, чтобы его начало совмещалось с концом вектора x (вектор y' ). Вектор z=x+y получится соединив начало x и конец вектора y'.

Рассмотрим процесс сложения векторов, начальные точки которых не совпадают с началом координат. На Рис.2 представлен процесс сложения векторов x=AB и y=CD, где A(1,1), B(10,-3), C(1,2), D(2,7). Из выражений (4) вычисляем координаты точки D':

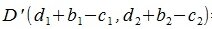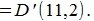Сумма векторов z=x+y будет иметь начальную точку A(1,1) и конечную точку D'(11,2).

Операция сложения векторов обладает следующими свойствами:

1. x+y=y+x (коммутативность).

2.(x+y)+w=x+(y+w) (ассоциативность).

3. x+0=x (наличие нулевого вектора).

4. x+(-x)=0 (наличие противоположного вектора).

Пример сложения двух векторов

Пример 1. Вычислить сумму векторов AB и CD, где A(2,2), B(7,6), C(5,6), D(10,7).

Вычислим новое расположение точек C и D, используя выражения (4). Тогда

C'(7,6), D'(10+7-5, 7+6-6)=D(12,7).

Сумма векторов AB и CD будет вектор AD', где A(2,2), D'(12,7).

Пример 2. Вычислить сумму векторов AB и у, где A(4,3), B(5,8), y=(7,3).

Так как вектор y представлен в виде координат, то это означает, что начальная точка вектора y является C(0,0) а конечная точка - D(7,3).

Вычисляя новое расположение вектора y, получим новые точки

C'(5,8), D'(7+5-0, 3+8-0)=D'(12,11).

Наконец, сумма векторов AB и y будет вектор AD', где A(4,3), D'(12,11).