Пусть в n-мерном пространстве задан ортонормированный базис
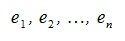
Как известно скалярное произведение ненулевых векторов x и y называется произведение
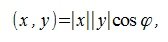 |
(1) |
где |·|-модуль вектора, φ -угол между векторами.
Если x=0 или y=0, то скалярное произведение равно нулю.
Вариант 1. Начальные точки всех векторов совпадают с началом координат.
Так как рассматривается пространство с ортонормированным базисом, то скалярное произведение можно вычислить также из выражения
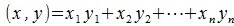 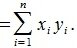 |
(2) |
где
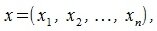 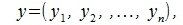 |
координаты векторов x и y соответственно.
Из выражений (1) и (2) следует, что косинус угла между двумя векторами равен
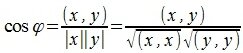 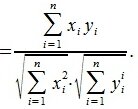 |
И, следовательно, угол между двумя векторами будет равен
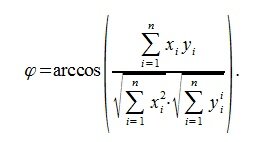
Вариант 2. Начальные точки векторов произвольные.
Пусть заданы векторы x=AB и y=CD, где 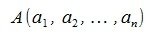 ,
,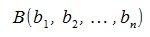 ,
,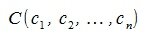 ,
,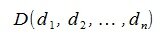 .
.
Переместим параллельно векторы x и y так, чтобы начальные точки векторов совпали с началом координат. Получим векторы x' и y' с координатами (т.е. с конечными точками):
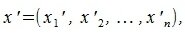 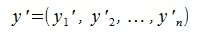 |
где
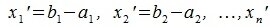 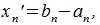 |
|
  |
При таком перемещении угол между векторами x и y равен углу между векторами x' и y'. Следовательно косинус угла между двумя векторами равен:
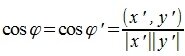 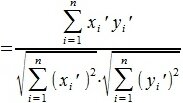 |
(3) |
Угол между двумя векторами будет равен:
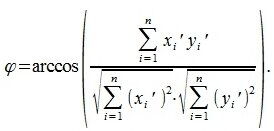 |
(4) |
Вариант 1. Начальные точки всех векторов совпадают с началом координат.
Пример . Найти угол между векторами x=(7,2) и y=(4,5).
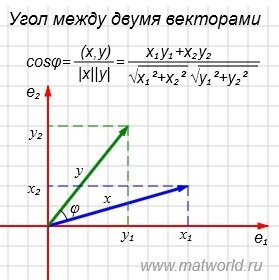
Рис. 1
На рисунке Рис. 1 в двухмерном пространстве представлены векторы x=(7,2) и y=(4,5).
Для вычисления угла между векторами x и y, вычислим нормы векторов x и y:
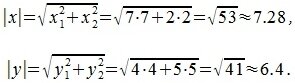
Косинус угла между векторами x и y, будет равен:
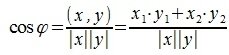 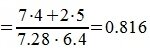 |
(5) |
Из выражения (5) вычисляем угол φ:
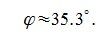
Вариант 2. Начальные точки векторов произвольные.
Пример . Найти угол между векторами x=AB и y=CD, где A(-1,1), B(3, 7), C(3,2), D(12,5).
На рисунке Рис. 2 в двухмерном пространстве представлены векторы x=AB и y=CD.
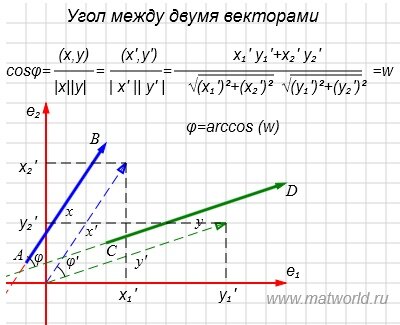
Рис. 2
Переместим параллельно векторы x и y так, чтобы начальные точки векторов совпали с началом координат. Получим векторы x' и y' с координатами (т.е. с конечными точками): x'=(3-(-1),7-1)=(4,6), y'=(12-3,5-2)=(9,3).
Угол φ между векторами x и y равен углу φ' между векторами x' и y'. Поэтому вычисляя угол φ' , получим угол между векторами x и y.
Вычислим норму векторов x' и y':
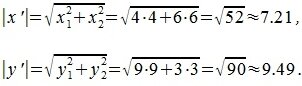
Косинус угла между векторами x' и y':
  |
Угол между двумя векторами будет равен:
