Определение 1. Если два числа1) a и b при делении на p дают один и тот же остаток r, то такие числа называются равноостаточными или сравнимыми по модулю p.
Утверждение 1. Пусть p какое нибудь положительное число. Тогда всякое число a всегда и притом единственным способом может быть представлено в виде
| a=sp+r, | (1) |
где s - число, и r одно из чисел 0,1, ..., p−1.
1) В данной статье под словом число будем понимать целое число.
Действительно. Если s получит значение от −∞ до +∞, то числа sp представляют собой совокупность всех чисел, кратных p. Рассмотрим числа между sp и (s+1)p=sp+p. Так как p целое положительное число, то между sp и sp+p находятся числа
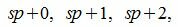 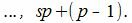 |
Но эти числа можно получить задав r равным 0, 1, 2,..., p−1. Следовательно sp+r=a получит всевозможные целые значения.
Покажем, что это представление единственно. Предположим, что p можно представить двумя способами a=sp+r и a=s1p+r1. Тогда
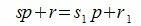 |
или
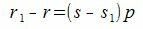 |
(2) |
Так как r1 принимает один из чисел 0,1, ..., p−1, то абсолютное значение r1−r меньше p. Но из (2) следует, что r1−r кратно p. Следовательно r1=r и s1=s.
Число r называется вычетом числа a по модулю p (другими словами, число r называется остатком от деления числа a на p).
Утверждение 2. Если два числа a и b сравнимы по модулю p, то a−b делится на p.
Действительно. Если два числа a и b сравнимы по модулю p, то они при делении на p имеют один и тот же остаток p. Тогда
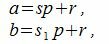 |
где s и s1 некоторые целые числа.
Разность этих чисел
 |
(3) |
делится на p, т.к. правая часть уравнения (3) делится на p.
Утверждение 3. Если разность двух чисел делится на p, то эти числа сравнимы по модулю p.
Доказательство. Обозначим через r и r1 остатки от деления a и b на p. Тогда
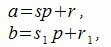 |
откуда
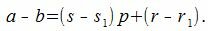 |
По утверждению a−b делится на p. Следовательно r−r1 тоже делится на p. Но т.к. r и r1 числа 0,1,..., p−1, то абсолютное значение |r−r1|<p. Тогда, для того, чтобы r−r1 делился на p должно выполнятся условие r=r1.
Из утверждения следует, что сравнимые числа - это такие числа, разность которых делится на модуль.
Если нужно записать, что числа a и b сравнимы между собой по модулю p, то пользуются обозначением (введенным Гауссом):
| a≡b mod(p) |
Примеры 25≡39 (mod 7), −18≡14 (mod 4).
Из первого примера следует, что 25 при делении на 7 дает тот же остаток, что и 39. Действительно 25=3·7+4 (остаток 4). 39=3·7+4 (остаток 4). При рассмотрении второго примера нужно учитывать, что остаток должен быть неотрицательным числом, меньшим, чем модуль (т.е. 4). Тогда можно записать: −18=−5·4+2 (остаток 2), 14=3·4+2 (остаток 2). Следовательно −18 при делении на 4 дает остаток 2, и 14 при делении на 4 дает остаток 2.
Свойство 1. Для любого a и p всегда
| a≡a mod (p). |
Свойство 2. Если два числа a и c сравнимы с числом b по модулю p , то a и c сравнимы между собой по тому же модулю, т.е. если
| a≡b mod (p), b≡c mod (p). |
то
| a≡c mod (p). |
Действительно. Из условия свойства 2 следует a−b и b−c делятся на p. Тогда их сумма a−b+(b−c)=a−c также делится на p.
Свойство 3. Если
| a≡b mod (p) и m≡n mod (p), |
то
| a+m≡b+n mod (p) и a−m≡b−n mod (p). |
Действительно. Так как a−b и m−n делятся на p, то
| (a−b)+ (m−n)=(a+m)−(b+n) , |
| (a−b)−(m−n)=(a−m)−(b−n) |
также делятся на p.
Это свойство можно распространить на какое угодно число сравнений, имеющих один и тот же модуль.
Свойство 4. Если
| a≡b mod (p) и m≡n mod (p), |
то
| am≡bn mod (p). |
Действительно.Так как a−b делится на p, то (a−b)m также делится на p, следовательно
| am≡bm mod (p). |
Далее m−n делится на p, следовательно b(m−n)=bm−bn также делится на p, значит
| bm≡bn mod (p). |
Таким образом два числа am и bn сравнимы по модулю с одним и тем же числом bm, следовательно они сравнимы между собой (свойство 2).
Свойство 5. Если
| a≡b mod (p). |
то
| ak≡bk mod (p). |
где k некоторое неотрицательное целое число.
Действительно. Имеем a≡b mod (p). Из свойства 4 следует
| a·a≡b·b mod (p). |
| a·a·a≡b·b·b mod (p). |
| ................. |
| ak≡bk mod (p). |
Все свойства 1-5 представить в следующем утверждении:
Утверждение 4. Пусть f(x1, x2, x3, ...) целая рациональная функция с целыми коэффициентами и пусть
| a1≡b1, a2≡b2, a3≡b3, ... mod (p). |
тогда
| f(a1, a2, a3, ...)≡f(b1, b2, b3, ...) mod (p). |
При делении все обстоит иначе. Из сравнения
| am≡bm mod (p) |
не всегда следует сравнение
| a≡b mod (p). |
Утверждение 5. Пусть
| am≡bm mod (p), |
тогда
| a≡b mod (p/λ), |
где λ это наибольший общий делитель чисел m и p.
Доказательство. Пусть λ наибольший общий делитель чисел m и p. Тогда
| m=m1λ и k=k1λ. |
Так как m(a−b) делится на k, то
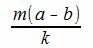 |
имеет нулевой остаток. Тогда
 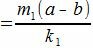 . . |
Следовательно
 |
имеет нулевой остаток, т.е. m1(a−b) делится на k1. Но числа m1 и k1 числа взаимно простые. Следовательно a−b делится на k1=k/λ и, тогда, a≡b mod (p/λ).
Утверждение 6. Если
| a≡b mod (p) |
и m является один из делителей числа p, то
| a≡b mod (m). |
Действительно. a−b делится на p. p делится на m. Следовательно a−b делится на m.
Утверждение 7. Если
| a≡b mod (p), a≡b mod (q), a≡b mod (s) |
то
| a≡b mod (h), |
где h наименьшее общее кратное чисел p,q,s.
Действительно. Разность a≡b должна быть числом, кратным p,q,s. и, следовательно должна быть кратным h.
В частном случае, если модули p,q,s взаимно простые числа, то
| a≡b mod (h), |
где h=pqs.
Заметим, что можно допустить сравнения по отрицательным модулям, т.е. сравнение a≡b mod (p) означает и в этом случае, что разность a−b делится на p. Все свойства сравнений остаются в силе и для отрицательных модулей.