Делимость чисел. Признак делимости

Определение 1. Пусть число a ¹) есть произведение двух чисел b и q так, что a=bq. Тогда a называется кратным b.

¹) В данной статье под словом число будем понимать целое число.

Можно сказать также a делится на b, или b есть делитель a, или b делит a, или b входит множителем в a.

Из определения 1 вытекают следующие утверждения:

Утверждение 1. Если a -кратное b, b-кратное c, то a кратное c.

Действительно. Так как

a=bm, b=nc,

где m и n какие то числа, то

a=(nc)m=(nm)c.

Следовательно a делится на c.

Если в ряду чисел, каждое делится на следующее за ним, то каждое число есть кратное всех последующих чисел.

Утверждение 2. Если числа a и b - кратные числа c, то их сумма и разность также кратные числа c.

Действительно. Так как

a=mc, b=nc,

тогда

a+b=mc+nc=(m+n)c,

a−b=mc−nc=(m−n)c.

Следовательно a+b делится на c и a−b делится на c .

Признаки делимости

Выведем общую формулу для определения признака делимости чисел на некоторое натуральное число m, которое называется признаком делимости Паскаля.

Найдем остатки деления на m следующей последовательностью. Пусть остаток от деления 10 на m будет r₁, 10·r₁ на m будет r₂, и т.д. Тогда можно записать:

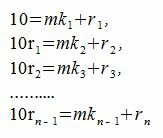(1)

Так как при делении любого числа на m остатки могут быть 0,1,...,m-1, то через m шагов остатки от деления на m будут повторяться (следовательно пересчитать их не нужно).

Любое натуральное число A в десятичной системе счисления можно представить в виде

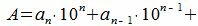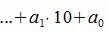(2)

Докажем, что остаток деления числа A на m равна остатку деления числа

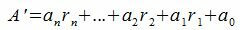(3)

на m.

Как известно, если два числа при делении на какое то число m дают одинаковый остаток, то из разность делится на m без остатка.

Рассмотрим разность A−A'

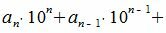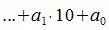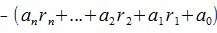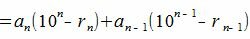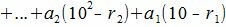(4)

Покажем, что 10ⁱ−r_i делиться на m при всех i=1,2,...m−1.

10−r_i=mk₁ делится на m (т.к. mk₁ кратно m),

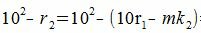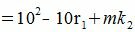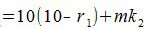(5)

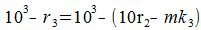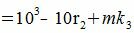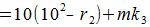(6)

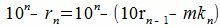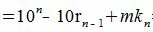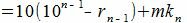(7)

Каждый член правой части (5) делится на m следовательно левая часть уравнения также делится на m. Рассуждая аналогично, получим - правая часть (6) делится на m, следовательно левая часть (6) также делится на m, правая часть (7) делится на m, следовательно левая часть (7) также делится на m. Получили, что правая часть уравнения (4) делится на m. Следовательно A и A' имеют одинаковый остаток при делении на m. В этом случае говорят, что A и A' равноостаточные или сравнимыми по модулю m.

Таким образом, если A' делится на m (имеет нулевой остаток от деления на m) , то A также делится на m (имеет нулевой остаток от деления на m). Мы показали что для определения делимости A можно определить делимость более простого числа A'.

Исходя из выражения (3), можно получить признаки делимости для конкретных чисел.

Признаки делимости чисел 2, 3, 4, 5, 6, 7, 8, 9, 10

Признак делимости на 2.

Следуя процедуре (1) для m=2, получим:

10=2·5+0, 10·0=2·5+0, и т.д.

Все остатки от деления на 2 равняются нулю. Тогда, из уравнения (3) имеем

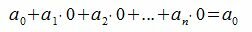Следовательно число делится на 2 тогда и только тогда, когда его последняя цифра делиться на 2 (т.е. когда число является четным).

Признак делимости на 3.

Следуя процедуре (1) для m=3, получим:

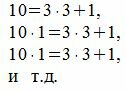Все остатки от деления на 3 равняются 1. Тогда, из уравнения (3) имеем

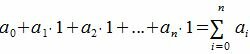Следовательно число делится на 3 тогда и только тогда, когда сумма всех его цифр делится на 3.

Признак делимости на 4.

Следуя процедуре (1) для m=4, получим:

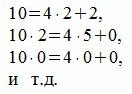Все остатки от деления на 4 кроме первого равняются 0. Тогда, из уравнения (3) имеем

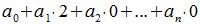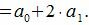Следовательно число делится на 4 тогда и только тогда, когда удвоенное число десятков сложенное с числом единиц делится на 4. Число делится на 4, если последние две цифры составляют число, делящееся на 4.

Признак делимости на 5.

Следуя процедуре (1) для m=5, получим:

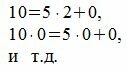Все остатки равны нулю. Тогда, из уравнения (3) имеем

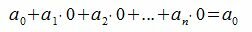Следовательно число делится на 5 тогда и только тогда, когда последняя цифра этого числа делится на 5, т.е. число оканчивается на 0 или 5.

Признак делимости на 6.

Следуя процедуре (1) для m=6, получим:

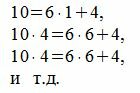Все остатки равны 4. Тогда, из уравнения (3) имеем

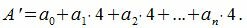Следовательно число делится на 6 тогда и только тогда, когда учетверённое число десятков, сложенное с числом единиц, делится на 6. То есть из числа отбрасываем правую цифру, далее суммируем полученное число с 4 и добавляем отброшенное число. Если данное число делится на 6, то исходное число делится на 6.

Пример. 2742 делится на 6, т.к. 274*4+2=1098, 1098=109*4+8=444, 444=44*4+4=180 делится на 6.

Более простой признак делимости. Число делится на 6, если оно делится на 2 и на 3 (т.е. если оно четное число и если сумма цифр делится на 3). Число 2742 делится на 6, т.к. число четное и 2+7+4+2=15 делится на 3.

Признак делимости на 7.

Следуя процедуре (1) для m=7, получим:

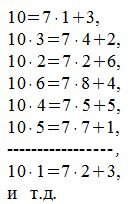Все остатки разные и повторяются через 7 шагов. Тогда, из уравнения (3) имеем

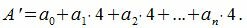(8)

Следовательно число делится на 7 тогда и только тогда, когда (8) делится на 7.

Пример. 3801 делится на 7, т.к. 1+0*3+8*2+3*6=1+16+18=35 делится на 7.

Другой признак делимости. Для определения, делится ли число на 7, из числа отбрасываем последнюю с права цифру, далее умножаем полученное число на 3 и добавляем и добавляет отброшенное число. Если данное число делится на 7, то исходное число делится на 6. 380*3+1=1141, 114*3+1=343, 34*3+3=105, 10*3+5=35 делится на 7, следовательно 3801 делится на 7.

Признак делимости на 8.

Следуя процедуре (1) для m=8, получим:

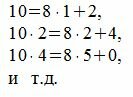Все остатки все остатки нулевые, кроме первых двух. Тогда, из уравнения (3) имеем

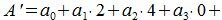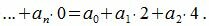(9)

Следовательно число делится на 8 тогда и только тогда, когда (9) делится на 8.

Пример. 4328 делится на 8, т.к. 8+2*2+4*3=24 делится на 8.

Признак делимости на 9.

Следуя процедуре (1) для m=9, получим:

Все остатки от деления на 9 равняются 1. Тогда, из уравнения (3) имеем

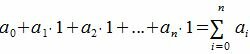Следовательно число делится на 9 тогда и только тогда, когда сумма всех его цифр делится на 9.

Признак делимости на 10.

Следуя процедуре (1) для m=10, получим:

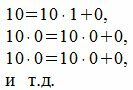Все остатки от деления на 10 равняются 0. Тогда, из уравнения (3) имеем

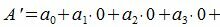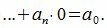Следовательно число делится на 10 тогда и только тогда, когда последняя цифра делится на 10 (то есть последняя цифра нулевая).