Определение 1. Простое число − это натуральное число больше единицы, которое делится только на себя и на 1.
Другими словами число является простым, если имеет только два различных натуральных делителя.
Определение 2. Любое натуральное число, которое кроме самого себя и единицы имеет и других делителей, называется составным числом.
Другими словами натуральные числа, не являющиеся простыми числами, называются составными. Из определения 1 следует, что составное число имеет больше двух натуральных делителей. Число 1 не является ни простым, ни составным т.к. имеет только один делитель 1 и, кроме этого многие теоремы относительно простых чисел не имеют места для единицы.
Из определений 1 и 2 следует, что каждое целое положительное число больше 1 является либо простым, либо составным числом.
Ниже представлена программа для отображения простых чисел до 5000. Заполните ячейки, нажмите на кнопку "Создать" и подождите несколько секунд.
| Простые числа до | |
| К-во столбцов в таблице | |
Утверждение 1. Если p - простое число и a любое целое число, то либо a делится на p, либо p и a взаимно простые числа.
Действительно. Если p простое число, то оно делится только на себя и на 1, если a не делится на p, то наибольший общий делитель a и p равен 1. Тогда p и a взаимно простые числа .
Утверждение 2. Если произведение нескольких чисел чисел a1, a2, a3, ... делится на простое число p, то по крайней мере одно из чисел a1, a2, a3, ... делится на p.
Действительно. Если бы ни одно из чисел не делилось на p, то числа a1, a2, a3, ... были бы взаимно простые числа по отношению p. Но из следствия 3 ( статья "Взаимно простые числа") следует, что их произведение a1, a2, a3, ... также взаимно простое по отношению к p, что противоречит условию утверждения. Следовательно по крайней мере один из чисел делится на p.
Теорема 1. Любое составное число всегда может быть представлено и притом единственным способом в виде произведения конечного числа простых чисел.
Доказательство. Пусть k составное число, и пусть a1 один из его делителей отличное от 1 и самого себя. Если a1 составное, то имеет кроме 1 и a1 и другой делитель a2. Если a2 число составное, то имеет кроме 1 и a2 и другой делитель a3. Рассуждая таким образом и учитывая, что числа a1, a2, a3, ... убывают и этот ряд содержит конечное число членов, мы дойдем какого-то простого числа p1. Тогда k можно представить в виде
| k=p1k1 |
Если k1 число простое, то k уже представлен в виде произведения простых чисел, в противном случае существует такое простое число p2, что
| k1=p2k2 |
Тогда
| k=p1p2k2. |
Если k2 число составное, то мы продолжаем процедуру до тех пор, пока k не будет представлено в виде произведения простых чисел:
| k=p1p2p3·... |
Первая часть теоремы доказана. Покажем, далее, что разложение составного числа на простые множители единственно (естественно, порядок множителей в произведении может быть другим).
Допустим существует два разложения числа k:
| k=p1p2p3..., k=q1q2q3..., |
(1) |
где pi (i=1,2,...), qj (j=1,2,...) простые числа. Из (1) следует, что
| p1p2p3...=q1q2q3... | (2) |
Так как k=p1p2p3... делится на простое число q1, то по крайней мере один из множителей, например p1 делится на q1. Но p1 простое число и делится только на 1 и на себя. Следовательно p1=q1 (т.к. q1≠1)
Тогда из (2) можно исключить p1 и q1:
| p2p3...=q2q3... |
Аналогичным способом можно доказать, что число q1 должно быть равно одному из простых чисел p2, p3, ... например p2, тогда
| p3...=q3... |
Таким образом убеждаемся, что всякое простое число входящее множителем в первое разложение один или несколько раз, входит и во второе разложение минимум столько же раз и наоборот, всякое простое число, которое входит множителем во второе разложение один или несколько раз входит и в первое разложение минимум столько же раз. Следовательно любое простое число входит множителем в оба разложения одинаковое число раз и, таким образом, эти два разложения одинаковы.■
Разложение составного числа k можно записать в следующем виде
 |
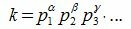(3) |
где p1, p2, ... различные простые числа, α, β, γ... целые положительные числа.
Разложение (3) называется каноническим разложением числа.
Простые числа в ряду натуральных чисел встречаются неравномерно. В одних частях ряда их больше, в других - меньше. Чем дальше мы продвигаемся по числовому ряду, тем реже встречаются простые числа. Возникает вопрос, существует ли самое большое простое число? Древнегреческий математик Евклид доказал, что простых чисел бесконечно много. Ниже мы представим это доказательство.
Теорема 2. Количество простых чисел бесконечно много.
Доказательство. Предположим, что существует конечное число простых чисел, и пусть наибольшее простое число равно p. Рассмотрим все числа больше p. По предположению утверждения эти числа должны быть составными и должны делится по крайней мере на один из простых чисел. Выберем число, являющиеся произведением всех этих простых чисел плюс 1:
| z=2·3·5·7·11···p+1 | (4) |
Число z больше p так как 2p уже больше p. p не делится ни на одно из этих простых чисел, т.к. при делении на каждое из них дает остаток 1. Таким образом мы приходим к противоречию. Следовательно существует бесчисленное множество простых чисел.
Данная теорема является частным случаем более общей теоремы:
Теорема 3. Пусть задана арифметическая прогрессия
| m, m+1d, m+2d, ... | (5) |
где d разность арифметической прогрессии, m первый член, и пусть d и m взаимно простые числа. Тогда арифметическая прогрессия (5) содержит бесконечное множество простых чисел.
Нетрудно заметить, что при m=1 и d=1 мы получим теорему 2.
Теорема 1 дает возможность определить, делится число m на n, если эти числа разложены на простые множители.
Если m делится на n, то n является кратным m:
| m=nq. |
Тогда любое простое число, входящее в n, должно входить и в m, поэтому в n не могут входить другие простые множители, которые не входят в m и притом эти простые множители в n входят не более число раз, чем в m.
Справедливо и обратное. Если каждый простой множитель числа n входит по крайней мере столько же раз в число m, то m делится на n.
Утверждение 3. Пусть a1,a2,a3,... различные простые числа входящие в m так, что
 |
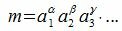Тогда все делители n числа m можно представить формулой
 |
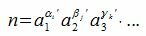(6) |
где i=0,1,...α, j=0,1,...,β, k=0,1,...,γ. Заметим, что αi принимает α+1 значений, βj принимает β+1 значений, γk принимает γ+1 значений, ... .
Каждая из чисел n вычисленная формулой (6) является делителем числа m.
Очевидно, при разных значениях i, j, k имеем разные делители числа m. Тогда число всех делителей m равно:
 |
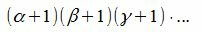Мы доказали следующую теорему:
Теорема 4. Пусть
|
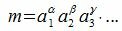каноническое разложение числа m. Тогда число делителей числа m равно:
|
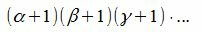Составим все произведения вида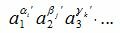 
, которые различны между собой и являются множеством всех делителей числа m. Найдем сумму этих делителей. Для этого запишем ряды чисел
 |
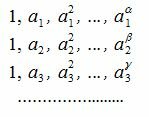Тогда для произведения вида 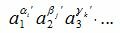берем по одному множителю из каждого горизонтального ряда. Используя правила умножения многочленов получим:
 |
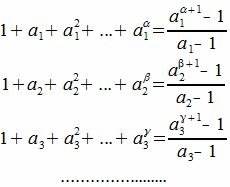Заметим, что правая часть каждой строки является суммой членов геометрической прогрессии.
Следовательно сумма всех делителей числа m равна
 |
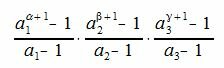(7) |
Мы доказали следующую теорему:
Теорема 5. Пусть
|
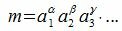каноническое разложение числа m. Тогда сумма всех делителей числа m равна выражению (7).
Пример . Возьмем число 280=23·5·7 .
Множество делителей этого числа такова
| 1 2 4 5 7 8 10 14 20 28 35 40 56 70 140 280 |
Число делителей числа 280 равно:
| (3+1)(1+1)(1+1)=16. |
Сумма делителей числа 280 равна:
 . |
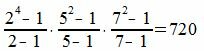