Наибольший общий делитель и наименьшее общее кратное. Онлайн калькулятор

Первое число: a=

Второе число: b=

Результат:

Наибольшее натуральное число, на которое делятся без остатка числа a и b, называется наибольшим общим делителем (НОД) этих чисел. Обозначается НОД(a,b), (a,b), gcd(a,b) или hcf(a,b).

Наименьшее общее кратное (НОК) двух целых чисел a и b есть наименьшее натуральное число, которое делится на a и b без остатка. Обозначается НОК(a,b), [a,b] или lcm(a,b).

Целые числа a и b называются взаимно простыми, если они не имеют никаких общих делителей кроме +1 и −1.

Наибольший общий делитель

Пусть даны два положительных числа a₁ и a₂¹). Требуется найти общий делитель этих чисел, т.е. найти такое число λ, которое делит числа a₁ и a₂ одновременно. Опишем алгоритм.

¹) В данной статье под словом число будем понимать целое число.

Пусть a₁ ≥ a₂, и пусть

,

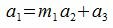где m₁, a₃ некоторые целые числа, a₃<a₂ (остаток от деления a₁ на a₂ должен быть меньше a₂).

Предположим, что λ делит a₁ и a₂, тогда λ делит m₁a₂ и λ делит a₁−m₁a₂=a₃ (Утверждение 2 статьи "Делимость чисел. Признак делимости"). Отсюда следует, что всякий общий делитель a₁ и a₂ является общим делителем a₂ и a₃. Справедливо и обратное, если λ общий делитель a₂ и a₃, то m₁a₂ и a₁=m₁a₂+a₃ также делятся на λ. Следовательно общий делитель a₂ и a₃ есть также общий делитель a₁ и a₂. Так как a₃<a₂≤a₁, то можно сказать, что решение задачи по нахождению общего делителя чисел a₁ и a₂ сведено к более простой задаче нахождения общего делителя чисел a₂ и a₃.

Если a₃≠0, то можно разделить a₂ на a₃. Тогда

,

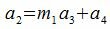где m₁ и a₄ некоторые целые числа, (a₄ остаток от деления a₂ на a₃(a₄<a₃)). Аналогичными рассуждениями мы приходим к выводу, что общие делители чисел a₃ и a₄ совпадают с общими делителями чисел a₂ и a₃, и также с общими делителями a₁ и a₂. Так как a₁, a₂, a₃, a₄, ... числа, постоянно убывающие, и так как существует конечное число целых чисел между a₂ и 0, то на каком то шаге n, остаток от деления a_n на a_n+1 будет равен нулю (a_n+2=0).

.

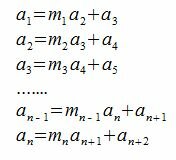Каждый общий делитель λ чисел a₁ и a₂ также делитель чисел a₂ и a₃, a₃ и a₄, .... a_n и a_n+1. Справедливо и обратное, общие делители чисел a_n и a_n+1 являются также делителями чисел a_n−1 и a_n, .... , a₂ и a₃, a₁ и a₂. Но общий делитель чисел a_n и a_n+1 является число a_n+1, т.к. a_n и a_n+1 без остатка делятся на a_n+1(вспомним, что a_n+2=0). Следовательно a_n+1 является и делителем чисел a₁ и a₂.

Отметим, что число a_n+1 является наибольшим из делителей чисел a_n и a_n+1, так как наибольший делитель a_n+1 является сам a_n+1. Если a_n+1 можно представить в виде произведения целых чисел, то эти числа также являются общими делителями чисел a₁ и a₂. Число a_n+1 называют наибольшим общим делителем чисел a₁ и a₂.

Числа a₁ и a₂ могут быть как положительными, так и отрицательными числами. Если один из чисел равен нулю, то наибольший общий делитель этих чисел будет равен абсолютной величине другого числа. Наибольший общий делитель нулевых чисел не определен.

Вышеизложенный алгоритм называется алгоритмом Евклида для нахождения наибольшего общего делителя двух целых чисел.

Пример нахождения наибольшего общего делителя двух чисел

Найти наибольший общий делитель двух чисел 630 и 434.

• Шаг 1. Делим число 630 на 434. Остаток 196.
• Шаг 2. Делим число 434 на 196. Остаток 42.
• Шаг 3. Делим число 196 на 42. Остаток 28.
• Шаг 4. Делим число 42 на 28. Остаток 14.
• Шаг 5. Делим число 28 на 14. Остаток 0.

На шаге 5 остаток от деления равен 0. Следовательно наибольший общий делитель чисел 630 и 434 равен 14. Заметим, что числа 2 и 7 также являются делителями чисел 630 и 434.

 Взаимно простые числа

Определение 1. Пусть наибольший общий делитель чисел a₁ и a₂ равен единице. Тогда эти числа называются взаимно простыми числами, не имеющими общего делителя.

Теорема 1. Если a₁ и a₂ взаимно простые числа, а λ какое то число, то любой общий делитель чисел λa₁ и a₂ является также общим делителем чисел λ и a₂.

Доказательство. Рассмотрим алгоритм Евклида для нахождения наибольшего общего делителя чисел a₁ и a₂ (см. выше).

.

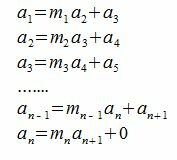Из условия теоремы следует, что наибольшим общим делителем чисел a₁ и a₂, и следовательно a_n и a_n+1 является 1. Т.е. a_n+1=1.

Умножим все эти равенства на λ, тогда

.

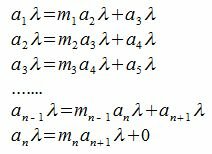Пусть общий делитель a₁λ и a₂ есть δ. Тогда δ входит множителем в a₁λ, m₁a₂λ и в a₁λ-m₁a₂λ=a₃λ (см. "Делимость чисел",Утверждение 2). Далее δ входит множителем в a₂λ и m₂a₃λ, и, следовательно, входит множителем в a₂λ-m₂a₃λ=a₄λ.

Рассуждая так мы убеждаемся, что δ входит множителем в a_n−1λ и m_n−1a_nλ, и , следовательно, в a_n−1λ−m_n−1a_nλ=a_n+1λ. Так как a_n+1=1, то δ входит множителем в λ. Следовательно число δ является общим делителем чисел λ и a₂.

Рассмотрим частные случаи теоремы 1.

Следствие 1. Пусть a и c простые числа относительно b. Тогда их произведение ac является простым числом относительно b.

Действительно. Из теоремы 1 ac и b имеют тех же общих делителей, что и c и b. Но числа c и b взаимно простые, т.е. имеют единственный общий делитель 1. Тогда ac и b также имеют единственный общий делитель 1. Следовательно ac и b взаимно простые.

Следствие 2. Пусть a и b взаимно простые числа и пусть b делит ak. Тогда b делит и k.

Действительно. Из условия утверждения ak и b имеют общий делитель b. В силу теоремы 1, b должен быть общим делителем b и k. Следовательно b делит k.

Следствие 1 можно обобщить.

Следствие 3. 1. Пусть числа a₁, a₂, a₃, ..., a_m простые относительно числа b. Тогда a₁a₂, a₁a₂·a₃, ..., a₁a₂a₃···a_m, произведение этих чисел простое относительно числа b.

2. Пусть имеем два ряда чисел

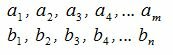
таких, что каждое число первого ряда простое по отношению каждого числа второго ряда. Тогда произведение

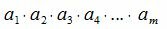	(1)

простое относительно каждого числа второго ряда. Таким образом все числа второго ряда простые относительно произведения (1). Следовательно их произведение

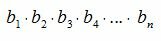
также простое относительно (1).

Следствие 4. Пусть числа a и b взаимно простые. Тогда любой степень числа a должен быть взаимно простой относительно любой степени числа b.

Действительно. Пусть в следствии 3

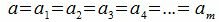и

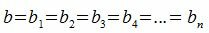Тогда a^m является взаимно простым числом относительно bⁿ.

Наименьшее общее кратное

Рассмотрим ряд чисел

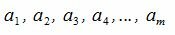Требуется найти такие числа, которые делятся на каждое из этих чисел.

Если число делится на a₁, то оно имеет вид sa₁, где s какое-нибудь число. Если q есть наибольший общий делитель чисел a₁ и a₂, то

a1=qa1',

a2=qa2',

где a₁' и a₂' числа взаимно простые (так как они не имеют общих делителей). Так как sa₁=sqa₁' должен делится на a₂=qa₂', то sa₁' должен делиться на a₂', и т.к. a₁' и a₂' числа взаимно простые, то в силу следствия 2, s должен делиться на a₂'. Тогда s должен иметь следующий вид

s=s1a2',

где s₁- некоторое целое число. Тогда

sa1=sqa1'=s1a2'a1'q.

(2)

То есть все числа кратные числам a₁ и a₂ должны иметь вид (2) и обратно, все числа вида (2) делятся и на a₁=qa₁', и на a₂=qa₂'. Но все числа кратные числам a₁ и a₂ являются кратными числа ε=a₂'a₁'q. Следовательно

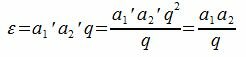является наименьшим общим кратным чисел a₁ и a₂.

В частном случае, когда числа a₁ и a₂ взаимно простые, то наименьшее общее кратное чисел a₁ и a₂:

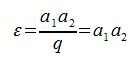(3)

как как наибольший общий делитель взаимно простых чисел q=1.

Наименьшее общее кратное трех и более чисел

Рассмотрим ряд чисел

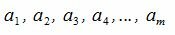Нужно найти наименьшее общее кратное этих чисел.

Из вышеизложенного следует, что любое кратное чисел a₁, a₂, a₃ должно быть кратным чисел ε и a₃, и обратно. Пусть наименьшее общее кратное чисел ε и a₃ есть ε₁. Далее, кратное чисел a₁, a₂, a₃, a₄ должно быть кратным чисел ε₁ и a₄. Пусть наименьшее общее кратное чисел ε₁ и a₄ есть ε₂. Таким образом выяснили, что все кратные чисел a₁, a₂, a₃,...,a_m совпадают с кратными некоторого определенного числа ε_n, которое называют наименьшим общим кратным данных чисел.

В частном случае, когда числа a₁, a₂, a₃,...,a_m взаимно простые, то наименьшее общее кратное чисел a₁, a₂ как было показано выше имеет вид (3). Далее, так как a₃ простое по отношению к числам a₁, a₂, тогда a₃ простое по отношению числа a₁·a₂ (Следствие 1). Значит наименьшее общее кратное чисел a₁,a₂,a₃ является число a₁ · a₂·a₃. Рассуждая аналогичным образом мы приходим к следующим утверждениям.

Утверждение 1. Наименьшее общее кратное взаимно простых чисел a₁, a₂, a₃,...,a_m равен их произведению a₁·a₂·a₃···a_m.

Утверждение 2. Любое число, которое делится на каждое из взаимно простых чисел a₁, a₂, a₃,...,a_m делится также на их произведение a₁·a₂·a₃···a_m.