Однородная система линейных уравнений

Рассмотрим систему линейных уравнений (СЛУ):

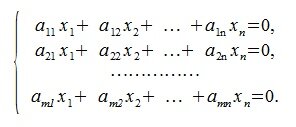(1)

Представим (1) в матричном виде:

Ax=0

(2)

где A m×n матрица, x вектор столбец порядка n , 0 - нулевой вектор столбец порядка m.

СЛУ (1) (или (2)) называется однородной системой линейных уравнений, т.к. правая часть системы равна нулю.

Однородная система линейных уравнений всегда совместна, т.к. вектор 0 всегда является решением системы (1):

A·0≡0.

Это решение называется нулевым или тривиальным решением.

Возникают вопросы :

1. Cистема линейных однородных уравнений имеет ли другие решения, кроме нулевого.
2. При каких условиях система линейных однородных уравнений имеет нетривиальное решение.
3. Как найти множество всех решений системы однородных линейных уравнений.

Если A n×n матрица и rank(A)=n, то нулевой вектор является единственным решением системы (1), в противном случае система имеет множество решений.

Обшее решение однородной системы линейных уравнений

Пусть A m×n - матрица rankA=r. В общем случае можем предположить что r<n, r<m. Тогда r столбцов матрицы A линейно независимы. Для удобства записи предположим, что это первые r столбцы матрицы A. Переставляя строки матрицы можно добиться того, чтобы подматрица матрицы A порядка r×r, расположенная в левом верхнем углу, была невырожденной. Запишем систему (2) в блочном виде:

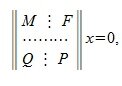(3)

где M - r×r - матрица, rang M=r.

Применяя метод исключения Гаусса для системы (3), получим:

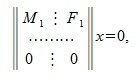(4)

где M₁ верхняя треугольная матрица, 0 - нулевые матрицы соответствующих порядков. Далее, применяя обратный ход исключения Гаусса, и, далее, разделив элементы каждой строки на ведущий элемент этой строки (если ведущий элемент существует) получим:

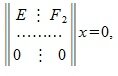(5)

где E - единичная матрица порядка r×r.

Рассмотрим матрицу

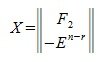(6)

где F₂- r×(n-r) - матрица, E^n-r- единичная матрица порядка n-r, X - матрица порядка n×(n-r).

В уравнении (5) вместо x подставляя матрицу (6), получим:

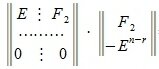(7)

Таким образом, векторы столбцы матрицы X являются решением системы (2) (или (1)). Более того, эти векторы линейно независимы и их линейная комбинация также является решением (2).

Общее решение системы однородных линейных уравнений имеет следующий вид:

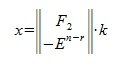(8)

гдe k - произвольный вектор столбец порядка n-r.

Общее решение системы однородных линейных уравнений можно также записать в следующем виде:

(9)

где x_i -i-ый вектор-столбец матрицы X, а k_i -i-ая координата вектора k

Множество всех решений (8)(или (9)) образует ядро или нуль пространство матрицы A и обозначается через Ker (A) или N(A).

В начале этого параграфа мы предполагали, что линейные независимые r векторы столбцы расположены в начале матрицы A. В общем случае, если они расположены в произвольных местах, аналогично вышеизложенному, применяя метод Гаусса, затем обратный ход Гауссова исключения и, наконец , разделив элементы каждой строки на ведущий элемент этой строки (если ведущий элемент существует), получим

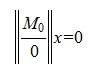(10)

Сделаем замену переменных:

(11)

где P -матрица перестановок поядка n×n выбрана так, чтобы при подстановке (11) в (10) получили:

(12)

где E - единичная матрица порядка r×r.

Аналогично вышеизложенному векторы столбцы матрицы X':

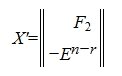(13)

образуют множесво всех решений однородной системы линейных уравнений (12).

Учитывая (11) получим:

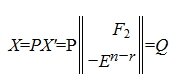Общее решение системы однородных линейных уравнений имеет следующий вид:

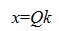(14)

гдe k - произвольный вектор столбец порядка n-r.

Общее решение системы однородных линейных уравнений можно также записать в следующем виде:

(15)

где q_i -i-ый вектор-столбец матрицы Q, а k_i -i-ая координата вектора k

Нахождение общего решения однородной системы линейных уравнений с помощью псевдообратной матрицы

Если rank(A)=r, r<n, то система (2) имеет множество решений, отличных от нуля и общее решение можно представить в следующем виде:

x=(E−A+A)z, для ∀z∈Rn,

(16)

где E —единичная матрица, A⁺ — псевдообратная к A матрица.

Для проверки подставим (16) в (2):

Ax=A(E−A⁺A)z=(A−AA⁺A)z=(A−A)z=0.

Ранг матрицы rank(E−A⁺A)=n-r. Следовательно столбцы матрицы E−A⁺A образуют множество всех решений системы (2).

Отметим, что r столбцов матрицы E−A⁺A линейно зависимы. Для исключения линейно зависимых столбцов можно сделать скелетное разложение. Тогда E−A⁺A=QS, где Q n×n−r - матрица rank(Q)=n−r, S n−r×n-матрица rank(S)=n−r. Тогда множество всех решений однородной системы линейных уравнений примет следующий вид:

где k=Sz.

Решение однородной системы линейных уравнений онлайн

Для решения однородной системы линейных уравнений пользуйтесь онлайн калькулятором который решает однородную систему по шагам и находит полное решение.