Метод исключения Гаусса
Рассмотрим следующую систему линейных уравнений:
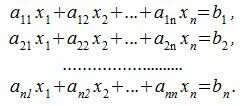 |
(1) |
Выберем в качестве ведущего элемента a11. Пусть 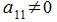 Исключим
Исключим 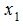 из уравнений (1), начиная со второго. Для этого первое уравнение умножим на
из уравнений (1), начиная со второго. Для этого первое уравнение умножим на 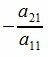 и прибавим ко второму . Затем первое уравнение умножим на
и прибавим ко второму . Затем первое уравнение умножим на 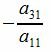 и прибавим к третьему и т.д. После этого вместо системы линейных уравнений (1) получим эквивалентную систему
и прибавим к третьему и т.д. После этого вместо системы линейных уравнений (1) получим эквивалентную систему
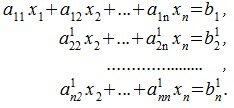 |
(2) |
где
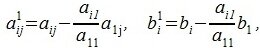 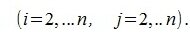 |
(3) |
Выберем в качестве ведущего элемента 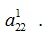 Пусть
Пусть 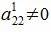 . Тогда аналогичным образом исключая x2 из последних n-2 уравнений системы (2), получим систему уравнений
. Тогда аналогичным образом исключая x2 из последних n-2 уравнений системы (2), получим систему уравнений
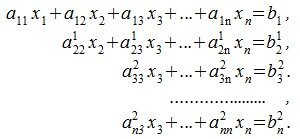 |
(4) |
Здесь 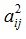 и
и 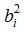 вычисляются из выражений
вычисляются из выражений
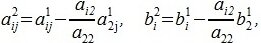 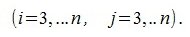 |
(5) |
Продолжая процесс, исходная система (1) примет следующий вид:
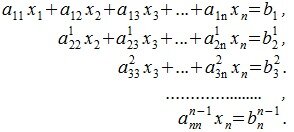 |
(6) |
Мы предполагаем, что
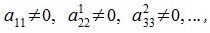 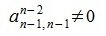 |
(7) |
Из последнего уравнения системы (6) вычисляем xn.
Если 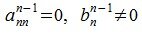 , система линейных уравнений (1) не имеет решение.
, система линейных уравнений (1) не имеет решение.
Если  , xn произвольное число.
, xn произвольное число.
Если 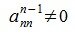 :
:
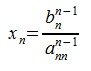
Подставляя найденное решение в (n-1) -е уравнение системы (6), получим искомую переменную xn-1. Подставляя xn-1 и xn в (n-2) -е уравнение получим переменную xn-2, и т.д.
Рассмотрим случай, когда условия (7) не выполняются. Очевидно, что при перестановке строк, решение системы линейных уравнений не меняется. Поэтому, если на каком то этапе преобразования ведущий элемент равен нулю, то можно переставлять строки. Переставлять строки рекомендуется и в случае, когда ведущий элемент близок к нулю. Более того, наилучший результат при решении системы получается при выборе максимального по модулю ведущего элемента.
Представим систему линейных уравнений (1) в матричном виде:
|
Ax=b,
|
(8) |
где  (i=1,2...n, j=1,2,...n), b=(b1 b2 ... bn)T, x=(x1,x2,... xn)T.
(i=1,2...n, j=1,2,...n), b=(b1 b2 ... bn)T, x=(x1,x2,... xn)T.
На первом этапе выберем максимальный по модулю ведущий элемент для первого столбца. Пусть он находится на k-ой строке. Тогда матрица перестановок получится из единичной матрицы порядка n, перестановкой первой и k-ой строк.

Тогда вместо системы (8) можно рассмотреть систему
|
P1Ax=P1b.
|
(9) |
Построим матрицу исключений:

Умножая левую и правую части системы (9) на M1, получим:
|
M1P1Ax=M1P1b.
|
(10) |
В системе (10) элементы первого столбца ниже ведущего элемента равны нулю. Таким образом первый шаг исключения закончен.
Во втором шаге аналогичным образом выбираются матрица перестановок P2 и матрица исключений M2. Вычисляются M2P2M1P1A и M2P2M1P1b . Стоится эквивалентная система
M2P2M1P1Ax=M2P2M1P1b
Через n-1 шагов получим:
MAx=Mb,
где 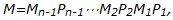 MA верхняя треугольная матрица.
MA верхняя треугольная матрица.
Далее, аналогично вышеизложенному, вычисляются xn, xn-1, ... x1.
Пример решения систем линейных уравнений методом исключения Гаусса
Рассмотрим следующую систему линейных уравнений:
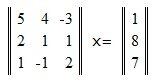 |
(11) |
Так как ведущий элемент 5 по модулю больше чем другие элементы в первом столбце, то матрица перестановок является единичной матрицей и, следовательно, P1A=EA=A, P1b=Eb=b, т.е. в системе (11) ничего не меняется.
Далее построим матрицу исключений M1:
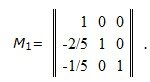
Вычисляя M1A и M1b, получим систему
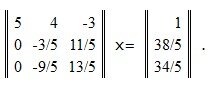
Так как |-3/5|<|-9/5|, переставим вторую и третью строки - для чего умножим левые и правые части уравнения (12) на матрицу перестановок
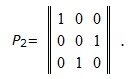
Тогда
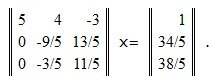 |
(13) |
Построим матрицу исключений M2:
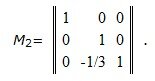
Умножая левые и правые части уравнения (13) на матрицу M2, получим:
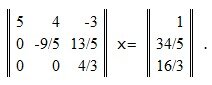 |
(14) |
Из последнего уравнения системы (14) вычислим x3:
x3=(16/3)/(4/3)=4.
Подставляя x3 во второе уравнение получим x2:
x2=(34/5−13/5*x3)/(-9/5)=2.
И, наконец, x1=(1-4*x2-(-3)*x3)/5=1.
Следовательно, решение системы линейных уравнений (11) является:
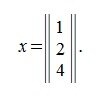 |
Для матричных вычислений пользуйтесь матричным онлайн калькулятором.