Разностью x-y векторов x и y называется вектор z такой, что z+y=x.
Вариант 1. Начальные точки всех векторов совпадают с началом координат.
Построим разность векторов 
и 
.
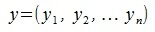Для построения разницы векторов z=x-y, нужно сложить вектор x с противоположным к y вектором y'. Противоположный вектор y' строится просто:
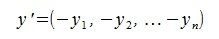
Вектор y' является противоположным к вектору y, так как y+y'=0, где 0 - нулевой вектор соответствующего размера. Далее выполняется сложение векторов x и y':
  |
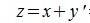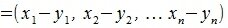Из выражения (1) видно что для построения разницы векторов достаточно вычислить разницы соответствующих координатов векторов x и y.
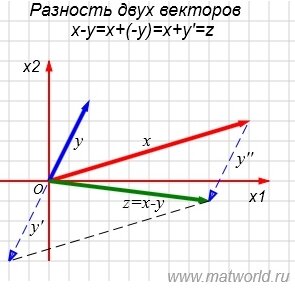
Рис. 1
На рисунке Рис. 1 в двухмерном пространстве представлен разность векторов x=(10,3) и y=(2,4).
Вычислим z=x-y=(10-3,3-4)=(7,-1). Сравним полученный результат с геометрической интерпретацией. Действительно, после построения вектора y' и параллельного перемещения начальной точки вектора y' на конечную точку вектора x, получим вектор y'', а после сложения векторов x и y'', получим вектор z.
Вариант 2. Начальные точки векторов произвольные.
В этом случае процесс вычисления разницы векторов не так очевиден. Для построения разницы векторов z=x-y, нужно сложить вектор x с противоположным к y вектором y'. Здесь в качестве противоположного к вектору y можно взять тот же вектор y и поменять направление вектора, изменив начальный и коненый точки местами. Можно также взять вектор y', который симметричен с y относительно начала координат. Если начальный и конечный точки вектора y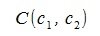 
и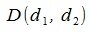 
, то начальный и конечный точки противоположного вектора y' будут 
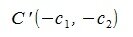и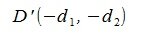 
соответственно. Таким образом для вычисления разницы векторов x и y, вычисляем сумму векторов x и y' (подробно см. в разделе сложение векторов).
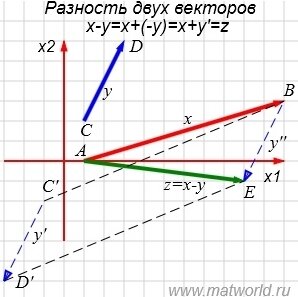
Рис. 2
На рисунке Рис. 2 в двухмерном пространстве представлен разность векторов x=AB и y=CD, где A(1,0), B(11,3), C(1,2), D(3,6). Для вычисления вектора z=x-y, построен противоположный к вектору y вектор y':
  |
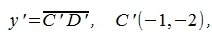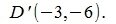Далее нужно сложить векторы x и y'. Вектор y' перемещается параллельно так, чтобы точка C' совпала с точкой B. Для этого вычисляются разницы координатов точек B и С:
 |
Получаем:
 |
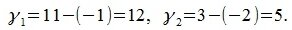Для перемещения точки D' на точку E, сделаем следующее преобразование координат точки D':
В результате получим вектор z=AE, A(1,0), E(9, -1), который является разницей векторов x=AB и y=CD.