Группа (математика)

Существуют математические объекты не являющиеся числами, но над ними мы имеем возможность совершать алгебраические действия. Свойства этих действий напоминают свойства действий над числами. Это делает необходимой сформулировать более общие понятия.

Определение 1. Полугруппой называется множество, в котором определено действие, сопоставляющее каждой упорядоченной паре элементов этого множества третий элемент − результат действия. Предполагается, что действие ассоциативно, т.е.

(a○b)○c=a○(b○c),

(1)

где ○− знак действия.

Примеры полугрупп

• множество целых неотрицательных чисел относительно сложения,
• множество целых неотрицательных чисел относительно умножения,
• множество классов по модулю относительно умножения.

Определение 2. Множество называется группой, если в нем определено действие, сопоставляющей каждой упорядоченной паре элементов третий элемент − результат действия и удовлетворяет следующим аксиомам:

1. (a○b)○c=a○(b○c), (операция ассоциативна).
2. Существует нейтральный элемент e такой, что при всех a из группы a○e=e○a=a.
3. Для каждого элемента a из группы существует обратный a⁻¹ такой, что a○a⁻¹=a⁻¹○ a=e.

В группе действие обычно обозначается как умножение (мультипликативная запись), а иногда как сложение (аддитивная запись). При мультипликативной записи нейтральный элемент обозначается 1, а при аддитивной записи 0. Обратный элемент при мультипликативной записи обозначается a⁻¹, а при аддитивной записи −a, и называется противоположным элементом.

Если операция коммутативна, т.е.

a○b=b○a,

то группа называется коммутативной или абелевой.

Рассмотрим примеры групп:

1. Множество всех целых чисел относительно сложения.

Действительно, операция сложения ассоциативна (a+b)+c=a+(b+c). Нейтральным элементом является 0 (a+0=0+a=a). Наконец, обратным для элемента а является −a ( a+(−a)=(−a)+a=0).

2. Множество положительных рациональных чисел относительно умножения.

Покажем, что это множество удовлетворяет всем трем пунктам определения 2. Ассоциативность очевидна ( (ab)c=a(bc) ). Нейтральным элементом является 1 ( a·1=1·a=a ).И, наконец, обратным элементом для a является ().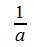

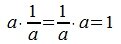3. Множество квадратных матриц относительно сложения.

Ассоциативность сложения очевидно следует из правил сложения матриц (a+b)+c=a+(b+c). Нейтральным элементом является нулевая матрица, а обратным (противоположным) элементом является нулевая матрица.

Все вышеизложенные примеры групп являются также коммутативными. Приведем пример некоммутативной группы.

4. Множество квадратных невырожденных матриц относительно умножения.

Действительно. Ассоциативность умножения матриц сохраняется. Нейтральным элементом является единичная матрица. Единичная матрица является невырожденной, умножение невырожденных матриц будет невырожденным, следовательно всегда существует обратная матрица. При множестве матриц порядка n≥2 мы имеем дело с некоммутативной группой т.к. умножение матриц в общем случае некоммутативна ab≠ba.