Симплекс метод онлайн

Симплекс метод

Симплекс метод − это метод решения задачи линейного программирования (ЗЛП). Суть метода заключается в нахождении начального допустимого плана, и в последующем улучшении плана до достижения максимального (или минимального) значения целевой функции в данном выпуклом многогранном множестве или выяснения неразрешимости задачи. Подробнее в статье: Решение задачи линейного программирования. Симплекс метод.

Примеры решения ЗЛП симплекс методом

Пример 1. Решить следующую задачу линейного программирования:

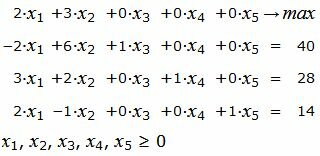Р е ш е н и е. Матрица коэффициентов 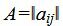системы уравнений имеет вид:

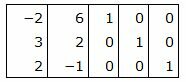Правая часть ограничений системы уравнений имеет вид:

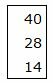Составляем симплексную таблицу. В столбец x₀ записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последняя строка - это целевая функция, умноженная на −1. Последние три векторы столбцы обазуют базис в трехмерном пространствое. Следовательно базисные переменные 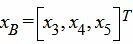, а свободные переменные :

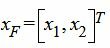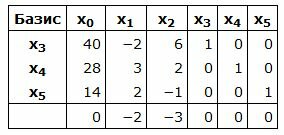Запишем текущий опорный план:

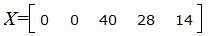Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-3), следовательно в базис входит вектор x₂. Определяем, какой вектор выходит из базиса. Для этого вычисляем 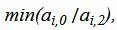при 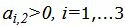. min(40:6, 28:2)=20/3 соответствует строке 1. Из базиса выходит вектор x₃. Сделаем исключение Гаусса для столбца x₂, учитывая, что ведущий элемент соответствует строке 1. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строки 2, 3, 4 со строкой 1, умноженной на -1/3, 1/6, 1/2, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.

Симплекс таблица примет следующий вид:

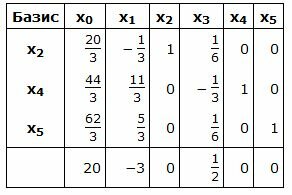Запишем текущий опорный план:

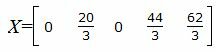Данный опорный план не является оптимальным, так как в последней строке есть отрицательный элемент (-3), следовательно в базис входит вектор x₁. Определяем, какой вектор выходит из базиса. Для этого вычисляем 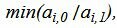при 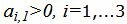. min(44/3:11/3, 62/3:5/3)=4 соответствует строке 2. Из базиса выходит вектор x₄. Сделаем исключение Гаусса для столбца x₁, учитывая, что ведущий элемент соответствует строке 2. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строки 1, 3, 4 со строкой 2, умноженной на 1/11, -5/11, 9/11, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.

Симплекс таблица примет следующий вид:

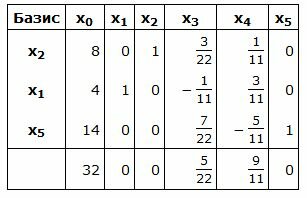Запишем текущий опорный план:

Текущий опорный план является оптимальным, так как в строках 4 под переменными 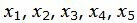нет отрицательных элементов.

Решение можно записать так: .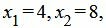

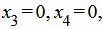
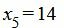Значение целевой функции в данной точке: F(X)=.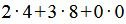

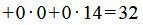Пример 2. Найти максимум функции

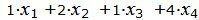при условиях

 

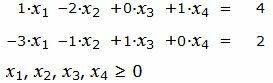Р е ш е н и е. Матрица коэффициентов 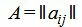системы уравнений имеет вид:

Правая часть ограничений системы уравнений имеет вид:

Составляем симплексную таблицу. В столбец x₀ записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последняя строка - это целевая функция, умноженная на −1:

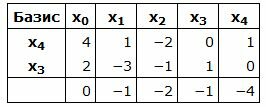Базисные векторы x₄, x₃, следовательно, все элементы в столбцах x₄, x₃, ниже горизонтальной линии должны быть нулевыми.

Обнулим все элементы столбца x₄, кроме ведущего элемента. Для этого сложим строку 3 со строкой 1, умноженной на 4. Обнулим все элементы столбца x₃, кроме ведущего элемента. Для этого сложим строку 3 со строкой 2, умноженной на 1.

Симплекс таблица примет вид:

 

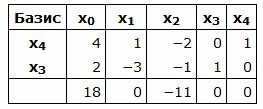Запишем текущий опорный план:

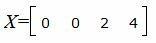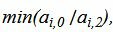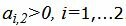Данный опорный план не является оптимальным, так как в последней строке есть отрицательный элемент (-11), следовательно в базис входит вектор x₂. Определяем, какой вектор выходит из базиса. Для этого вычисляем при . Все 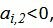следовательно целевая функция неограничена сверху. Т.е. задача линейного программирования неразрешима.

Примеры решения ЗЛП методом искусственного базиса

Пример 1. Найти максимум функции

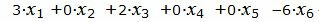при условиях

 

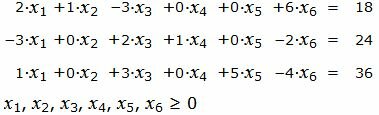Р е ш е н и е. Так как количество базисных векторов должен быть 3, то добавляем искусственное переменное, а в целевую функцию добавляем это переменное, умноженное на −M, где M, очень большое число:

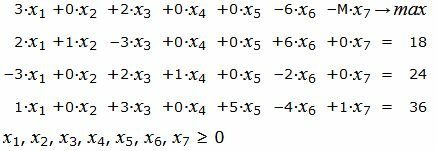Матрица коэффициентов 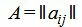системы уравнений имеет вид:

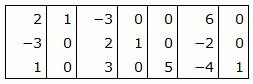Правая часть ограничений системы уравнений имеет вид:

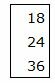Составляем симплексную таблицу. В столбец x₀ записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последние две строки − это целевая функция, умноженная на −1 и разделенная на две части. Последняя строка − строка с исскуственными переменными:

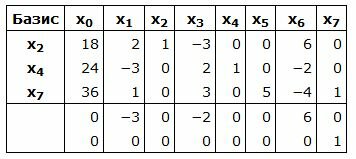Базисные векторы 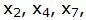следовательно, все элементы в столбцах 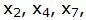ниже горизонтальной линии должны быть нулевыми.

Обнулим все элементы столбца 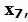кроме ведущего элемента. Для этого сложим строку 5 со строкой 3, умноженной на -1.

Симплекс таблица примет вид:

 

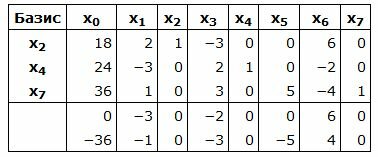Запишем текущий опорный план:

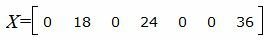Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-5), следовательно в базис входит вектор 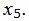Определяем, какой вектор выходит из базиса. Для этого вычисляем 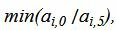при 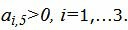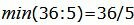соответствует строке 3. Из базиса выходит вектор 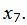Сделаем исключение Гаусса для столбца 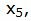учитывая, что ведущий элемент соответствует строке 3. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строку 5 со строкой 3, умноженной на 1. Далее делим строку с ведущим элементом на ведущий элемент.

Симплекс таблица примет следующий вид:

 

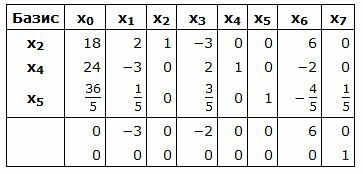Запишем текущий опорный план:

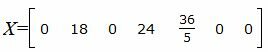Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-3), следовательно в базис входит вектор 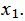Определяем, какой вектор выходит из базиса. Для этого вычисляем при 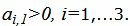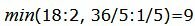соответствует строке 1. Из базиса выходит вектор x₂. Сделаем исключение Гаусса для столбца x₁, учитывая, что ведущий элемент соответствует строке 1. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строки 2, 3, 4 со строкой 1, умноженной на 3/2, -1/10, 3/2, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.

Симплекс таблица примет следующий вид:

 

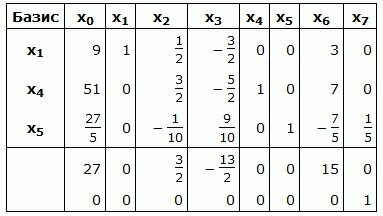Запишем текущий опорный план:

Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-13/2), следовательно в базис входит вектор x₃. Определяем, какой вектор выходит из базиса. Для этого вычисляем 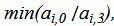при 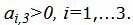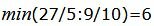соответствует строке 3. Из базиса выходит вектор x₅. Сделаем исключение Гаусса для столбца x₃, учитывая, что ведущий элемент соответствует строке 3. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строки 1, 2, 4 со строкой 3, умноженной на 5/3, 25/9, 65/9, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.

Симплекс таблица примет следующий вид:

 

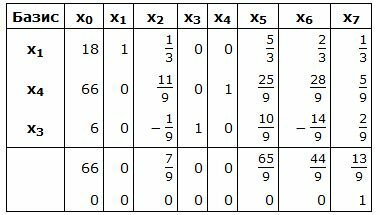Запишем текущий опорный план:

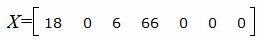Текущий опорный план является оптимальным, так как в строках 4−5 под переменными 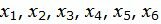нет отрицательных элементов.

Решение исходной задачи можно записать так:

.

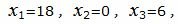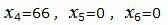Значение целевой функции в данной точке:

.

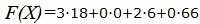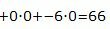Пример 2. Найти оптимальный план задачи линейного программирования:

 

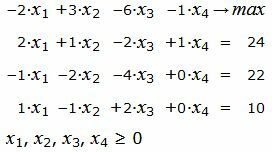Р е ш е н и е. Так как количество базисных векторов должен быть 3, то добавляем искусственные переменные, а в целевую функцию добавляем эти переменные, умноженные на −M, где M, очень большое число:

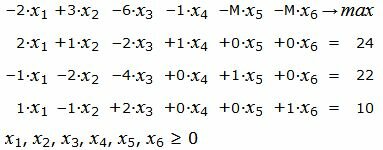Матрица коэффициентов 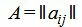системы уравнений имеет вид:

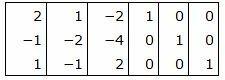Правая часть ограничений системы уравнений имеет вид:

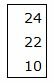Составляем симплексную таблицу. В столбец x₀ записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последние две строки − это целевая функция, умноженная на −1 и разделенная на две части. Последняя строка − строка с исскуственными переменными:

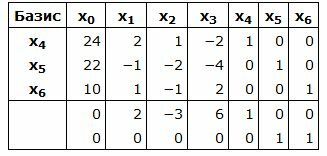Базисные векторы x₄, x₅, x₆, следовательно, все элементы в столбцах x₄, x₅, x₆, ниже горизонтальной линии должны быть нулевыми.

Обнулим все элементы столбца x₄, кроме ведущего элемента. Для этого сложим строку 4 со строкой 1, умноженной на -1. Обнулим все элементы столбца x₅, кроме ведущего элемента. Для этого сложим строку 5 со строкой 2, умноженной на -1. Обнулим все элементы столбца x₆, кроме ведущего элемента. Для этого сложим строку 5 со строкой 3, умноженной на -1.

Симплекс таблица примет вид:

 

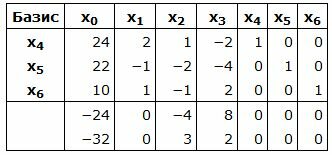Запишем текущий опорный план:

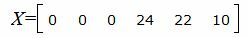В строке 5 элементы, соответствующие переменным x₁, x₂, x₃, x₄, x₅, x₆ неотрицательны, а число находящийся в пересечении данной строки и столбца x₀ отрицательнo. Тогда исходная задача не имеет опорного плана. Следовательно она неразрешима.